Đạo Hàm Là Gì? Khái Niệm Và Các Công Thức Đạo Hàm Cơ Bản Đến Nâng Cao

1. Định nghĩa đạo hàm 

Đạo hàm là một khái niệm trong toán học để mô tả sự biến đổi của một hàm số khi biến số độc lập (thường là 

𝑥

x) thay đổi. Nó cho biết tỉ lệ thay đổi của giá trị của hàm số tại một điểm cụ thể khi biến số này thay đổi một lượng rất nhỏ. Đạo hàm của một hàm số được tính bằng cách lấy độ chia lớn nhất của tỷ số của sự thay đổi của hàm số và biến số độc lập tại điểm đó. Nếu giá trị đạo hàm là dương, hàm số đang tăng tại điểm đó; nếu là âm, hàm số đang giảm. Đạo hàm cũng có thể được sử dụng để xác định các điểm cực trị của hàm số, nơi hàm số có cực đại hoặc cực tiểu. Trong thực tế, công thức đạo hàm có nhiều ứng dụng quan trọng, từ tối ưu hóa trong kinh tế đến dự báo xu hướng trong khoa học dữ liệu và vật lý. Nó là công cụ mạnh mẽ trong việc hiểu và mô hình hóa các quy luật tự nhiên và các hiện tượng biến đổi.

Học sinh giờ toán

2. Quy tắc tính đạo hàm 

Quy tắc tính đạo hàm là một tập hợp các quy tắc và phương pháp để tính đạo hàm của các hàm số. Nó được sử dụng để xác định tỉ lệ thay đổi của giá trị của một hàm số khi biến số độc lập thay đổi. Các quy tắc này giúp chúng ta tính toán đạo hàm một cách hiệu quả và chính xác.

Một trong những quy tắc cơ bản là quy tắc tổng, cho phép tính đạo hàm của tổng của hai hàm số. Quy tắc này nói rằng đạo hàm của tổng của hai hàm số bằng tổng của các đạo hàm của từng hàm số đó.

Một quy tắc khác là quy tắc tích, giúp tính đạo hàm của tích của hai hàm số. Quy tắc này sử dụng tổ hợp đạo hàm của các thành phần trong tích để tính toán.

Các quy tắc còn bao gồm quy tắc thương, dùng để tính đạo hàm của thương của hai hàm số, và quy tắc chuỗi, dùng cho các hàm hợp (composite functions). Quy tắc chuỗi là phương pháp để tính đạo hàm của một hàm hợp của hai hàm số, trong đó mỗi hàm là hàm của biến số khác nhau.

Việc áp dụng các quy tắc này giúp chúng ta phân tích hàm số và tìm ra các thông tin quan trọng như điểm cực trị (cực đại, cực tiểu), điều kiện tối ưu, và các đặc tính khác của hàm số. Các quy tắc này là công cụ quan trọng trong toán học ứng dụng, khoa học, kỹ thuật, và nhiều lĩnh vực khác. Chúng giúp ta hiểu sâu hơn về các quy luật tự nhiên và dự báo các biến đổi trong thực tế.

Tham khảo:  Đội hình man Utd gặp Man city
 

3. Ứng dụng và ý nghĩa đạo hàm

Các quy tắc tính đạo hàm là công cụ quan trọng trong việc tối ưu hóa, dự báo, và mô hình hóa các quy luật tự nhiên trong nhiều lĩnh vực khoa học và kỹ thuật. Chúng giúp chúng ta phân tích và dự đoán các biến đổi trong thực tế, từ nghiên cứu thị trường đến phát triển công nghệ mới. Hiểu biết về các quy tắc này không chỉ giúp gia tăng khả năng giải quyết các vấn đề phức tạp mà còn mở ra những cơ hội mới trong sự nghiệp và nghiên cứu toán học.

Các công thức đạo hàm cần nhớ

Công thức đạo hàm sơ cấp

Công thức đạo hàm tổng quát 

Công thức đạo hàm cấp cao

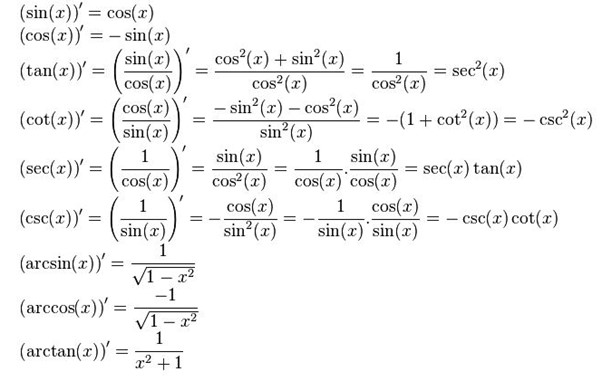
Công thức đạo hàm lượng giác

4. Một số câu hỏi thường gặp về đạo hàm 

Dưới đây là một số câu hỏi thường gặp về đạo hàm cùng với câu trả lời mô tả chung về từng câu hỏi:

Câu hỏi: Đạo hàm là gì và tại sao lại quan trọng trong toán học?

Câu trả lời: Đạo hàm là một khái niệm trong toán học biểu thị sự biến thiên của một hàm số. Nó cho biết tốc độ thay đổi của hàm số tại một điểm cụ thể. Qua đạo hàm, chúng ta có thể tìm ra các điểm cực trị, xác định độ dốc của đồ thị hàm số và giải quyết các vấn đề về tối ưu hóa.

Câu hỏi: Làm thế nào để tính đạo hàm của một hàm số?

Câu trả lời: Để tính đạo hàm của một hàm số, chúng ta sử dụng quy tắc đạo hàm, tức là các quy tắc và công thức để xác định sự biến thiên của hàm số. Cách tính này tùy thuộc vào loại hàm số và quy tắc cụ thể áp dụng cho từng trường hợp.

Câu hỏi: Tại sao đạo hàm lại được sử dụng để tìm điểm cực trị của một hàm số?

Câu trả lời: Đạo hàm của một hàm số cho biết điểm mà hàm số có độ dốc bằng không (điểm cực trị). Bằng cách tìm các điểm mà đạo hàm bằng không và kiểm tra sự biến đổi của đạo hàm xung quanh các điểm này, chúng ta có thể xác định các điểm cực trị của hàm số.

Câu hỏi: Đạo hàm có ứng dụng trong các lĩnh vực nào ngoài toán học?

Câu trả lời: Đạo hàm được áp dụng rộng rãi trong nhiều lĩnh vực như vật lý, kỹ thuật, kinh tế học, khoa học máy tính và nhiều lĩnh vực khoa học khác. Nó giúp trong việc mô hình hóa và giải quyết các vấn đề thực tế, từ tối ưu hóa chi phí đến dự đoán xu hướng và hiệu suất của các hệ thống.

Câu hỏi: Đạo hàm bậc hai có ý nghĩa gì?

Câu trả lời: Đạo hàm bậc hai của một hàm số cho biết sự biến thiên của đạo hàm cấp một của hàm số. Nó cho ta thông tin về độ cong của đồ thị hàm số và được sử dụng để xác định các điểm uốn lõm và uốn lên trên đồ thị hàm số.

Câu hỏi: Làm thế nào để áp dụng đạo hàm vào giải quyết các vấn đề thực tế?

Câu trả lời: Đạo hàm được sử dụng để tối ưu hóa hàm mục tiêu, giải quyết các bài toán về tốc độ, gia tốc, cấu trúc tối ưu của hệ thống, và nhiều ứng dụng khác trong thực tế. Việc áp dụng đạo hàm giúp tối ưu hóa các quyết định và cải thiện hiệu quả của các quy trình.

Các câu hỏi và câu trả lời trên giúp bạn hiểu rõ hơn về ý nghĩa và ứng dụng của đạo hàm trong các lĩnh vực khác nhau, mà không cần liệt kê các công thức cụ thể.