-
-
-
Tổng tiền thanh toán:
-
Tổng Hợp Công Thức Đạo Hàm Cơ Bản Và Cấp Cao
Ngày đăng:
04/12/2024
Bởi: CÔNG TY CỔ PHẦN THƯƠNG MẠI VÀ ĐÀU TƯ -HELIOS
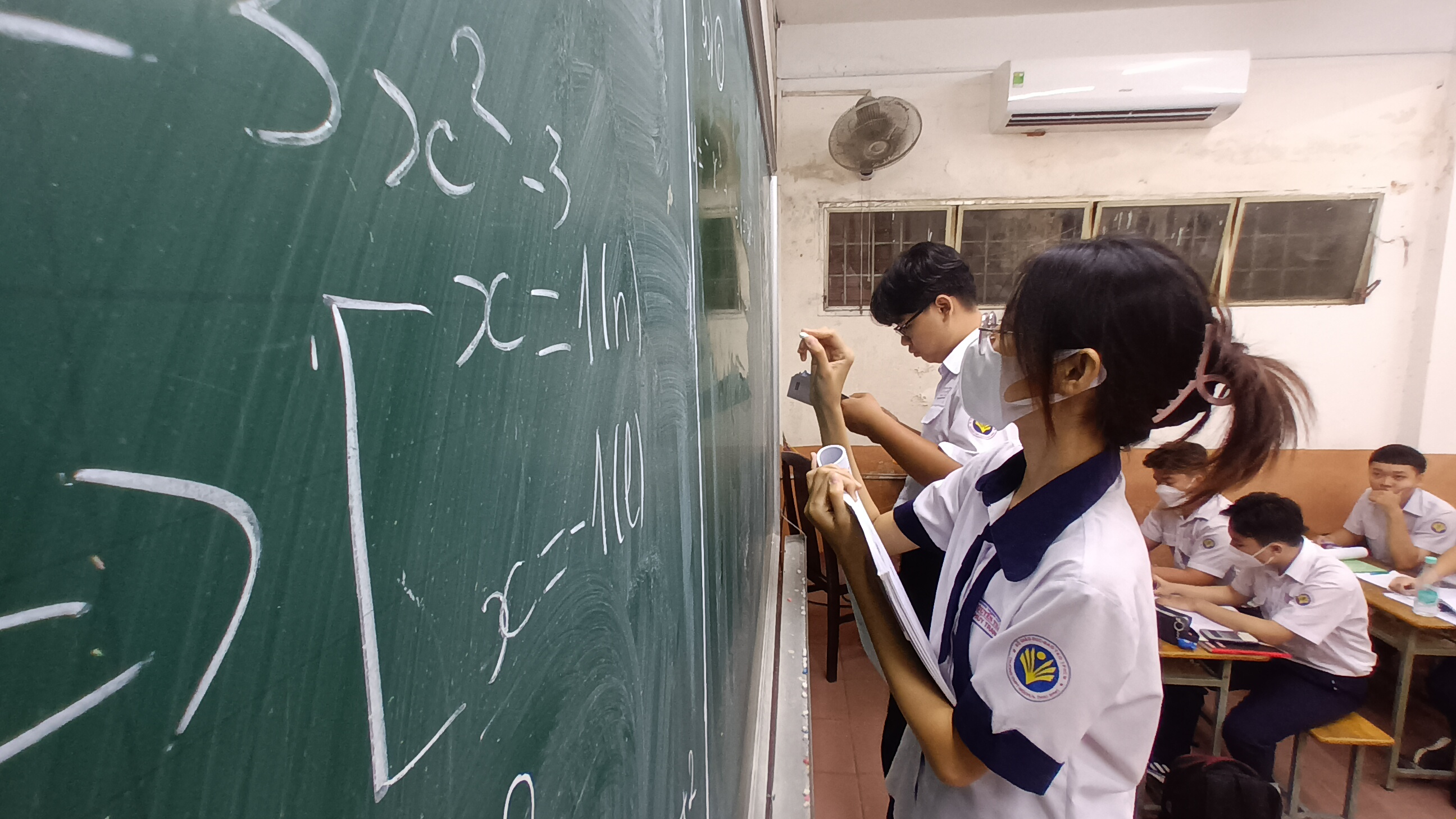
|
[MỤC LỤC]
|
1. Định nghĩa đạo hàm
Đạo hàm của một hàm số tại một điểm cho biết tốc độ thay đổi của hàm số đó tại điểm đó, hay nói cách khác, đạo hàm mô tả độ dốc của đồ thị hàm số tại điểm xét. Đạo hàm là một khái niệm quan trọng trong giải tích, công thức đạo hàm giúp ta hiểu được sự biến thiên của một hàm số theo biến độc lập.
2. Công thức đạo hàm tổng quát

Công thức cơ bản

Công thức lượng giác
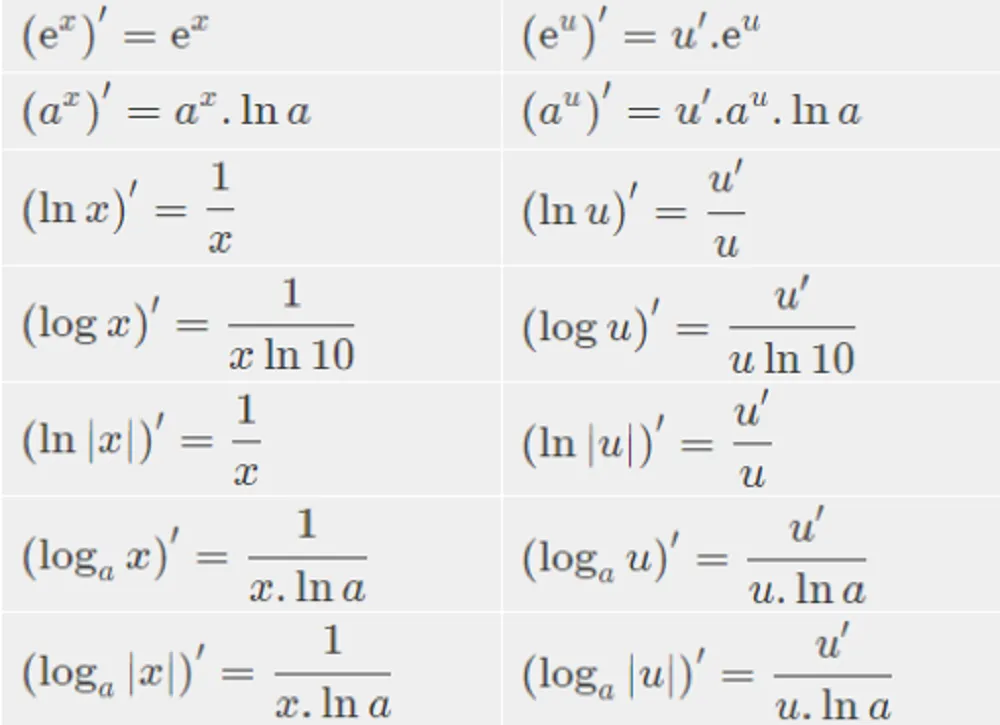
Công thức ĐH logorit
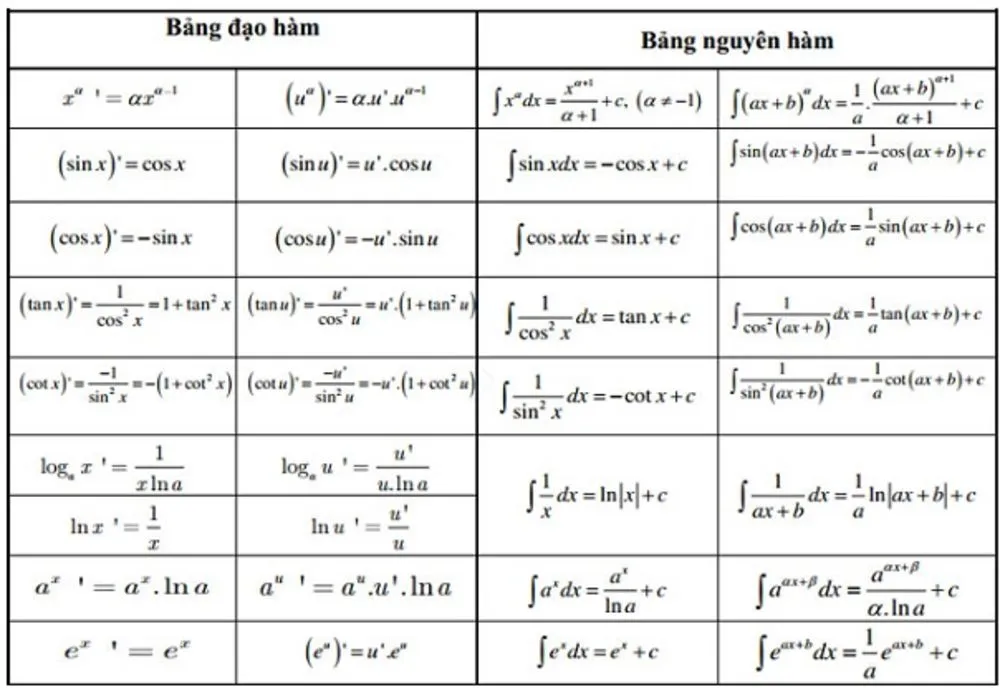
Bảng đạo hàm và nguyên hàm
3. Ứng dụng đạo hàm
Đạo hàm có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau của toán học và thực tế, giúp mô tả và giải quyết các vấn đề liên quan đến sự thay đổi và tối ưu hóa. Dưới đây là một số ứng dụng phổ biến của đạo hàm:
Xác định độ dốc và phương trình tiếp tuyến:
Đạo hàm giúp xác định độ dốc của đồ thị hàm số tại một điểm. Độ dốc này là độ nghiêng của đường tiếp tuyến tại điểm đó.
Phương trình tiếp tuyến của đồ thị hàm số tại điểm x=ax = ax=a có dạng:
y−f(a)=f′(a)(x−a)y - f(a) = f'(a)(x - a)y−f(a)=f′(a)(x−a) Điều này có ích trong việc mô phỏng sự thay đổi của một hàm số tại các điểm cụ thể.
Tìm cực trị (maxima và minima) của hàm số:
Đạo hàm được sử dụng để tìm các điểm cực trị của hàm số (điểm cực đại và cực tiểu).
Quy trình:
Tìm đạo hàm của hàm số và giải phương trình f′(x)=0f'(x) = 0f′(x)=0 để xác định các điểm nghi ngờ là cực trị.
Sử dụng đạo hàm bậc hai f′′(x)f''(x)f′′(x) để kiểm tra xem điểm đó là cực đại hay cực tiểu:
Nếu f′′(x)>0f''(x) > 0f′′(x)>0, điểm đó là cực tiểu.
Nếu f′′(x)<0f''(x) < 0f′′(x)<0, điểm đó là cực đại.
Tính toán tốc độ thay đổi trong vật lý:
Trong vật lý, đạo hàm được sử dụng để mô tả sự thay đổi của các đại lượng theo thời gian, chẳng hạn như:
Tốc độ (đạo hàm của vị trí theo thời gian).
Gia tốc (đạo hàm của tốc độ theo thời gian).
Ví dụ: Nếu vị trí của một vật là x(t)x(t)x(t), thì tốc độ là v(t)=x′(t)v(t) = x'(t)v(t)=x′(t), và gia tốc là a(t)=v′(t)=x′′(t)a(t) = v'(t) = x''(t)a(t)=v′(t)=x′′(t).
Tính toán độ dốc trong các bài toán tối ưu hóa:
Đạo hàm được sử dụng trong các bài toán tối ưu hóa để tìm giá trị tối ưu (tối đa hoặc tối thiểu) của một hàm số, chẳng hạn trong việc tối đa hóa lợi nhuận, tối thiểu hóa chi phí, hay thiết kế các hệ thống tối ưu trong kỹ thuật.
Quá trình này liên quan đến việc tìm đạo hàm bậc nhất và giải phương trình f′(x)=0f'(x) = 0f′(x)=0 để tìm các điểm cực trị, sau đó phân tích chúng.
Giải phương trình vi phân:
Đạo hàm là công cụ quan trọng trong việc giải các phương trình vi phân, nơi mà hàm số phải thỏa mãn một mối quan hệ với đạo hàm của nó. Các phương trình vi phân xuất hiện trong nhiều lĩnh vực như động học, nhiệt động lực học, kinh tế học, v.v.
Mô phỏng sự thay đổi trong các mô hình toán học và khoa học máy tính:
Trong khoa học máy tính và mô phỏng, đạo hàm được sử dụng để tính toán và tối ưu hóa các mô hình mô phỏng, chẳng hạn như trong học máy (machine learning) để tối ưu hóa các hàm mất mát (loss function).
Ứng dụng trong kinh tế học:
Đạo hàm được sử dụng để phân tích các yếu tố như sản lượng, chi phí, lợi nhuận và năng suất. Ví dụ:
Tính toán điểm hòa vốn: Đạo hàm của hàm lợi nhuận hoặc chi phí giúp xác định số lượng sản phẩm cần sản xuất để tối đa hóa lợi nhuận hoặc tối thiểu hóa chi phí.
Lợi tức cận biên: Đạo hàm giúp xác định mức độ thay đổi của lợi ích khi gia tăng một đơn vị đầu vào, ví dụ như lao động hoặc vốn.
Ứng dụng trong sinh học và y học:
Đạo hàm được sử dụng trong mô hình hóa sự phát triển của quần thể sinh học, tốc độ lây lan dịch bệnh, hay quá trình phục hồi sau khi điều trị bệnh.
Ví dụ, trong mô hình tăng trưởng quần thể, đạo hàm có thể giúp tính toán tốc độ thay đổi của số lượng cá thể trong quần thể theo thời gian.
Ứng dụng trong thiết kế kỹ thuật và xây dựng:
Trong thiết kế kỹ thuật, đạo hàm được sử dụng để tính toán các yếu tố như độ cứng của vật liệu, sự thay đổi nhiệt độ, hoặc áp lực tác động lên một vật thể khi thiết kế máy móc, cầu, hoặc các công trình xây dựng.
Phân tích sự thay đổi trong hóa học:
Đạo hàm giúp phân tích tốc độ phản ứng trong hóa học, như tốc độ thay đổi nồng độ của các chất phản ứng trong một phản ứng hóa học, hoặc xác định các điểm cân bằng hóa học trong các phản ứng.
>> Tham khảo: Nhị thức newton

Học sinh trao đổi sau giờ học
4. Một số câu hỏi thường gặp về Đạo Hàm
Dưới đây là một số câu hỏi thường gặp về đạo hàm:
**Đạo hàm là gì?**
- **Trả lời:** Đạo hàm của một hàm số tại một điểm là tốc độ thay đổi của giá trị hàm tại điểm đó. Nó có thể được hiểu là độ dốc của đường tiếp tuyến với đồ thị của hàm tại điểm đó.
**Công thức đạo hàm cơ bản là gì?**
- **Trả lời:** Một số công thức đạo hàm cơ bản bao gồm:
- Đạo hàm của một hằng số: \( \frac{d}{dx} (c) = 0 \)
- Đạo hàm của \( x^n \): \( \frac{d}{dx}(x^n) = n \cdot x^{n-1} \)
- Đạo hàm của hàm số mũ: \( \frac{d}{dx}(e^x) = e^x \)
- Đạo hàm của hàm số lượng giác:
- \( \frac{d}{dx}(\sin x) = \cos x \)
- \( \frac{d}{dx}(\cos x) = -\sin x \)
- Đạo hàm của hàm số logarithm: \( \frac{d}{dx}(\ln x) = \frac{1}{x} \)
**Đạo hàm có ý nghĩa gì trong thực tế?**
- **Trả lời:** Đạo hàm giúp ta hiểu sự thay đổi của một đại lượng theo một biến độc lập. Trong vật lý, đạo hàm có thể đại diện cho tốc độ hoặc gia tốc, trong kinh tế học, đạo hàm giúp xác định các điểm tối ưu, như tối đa hóa lợi nhuận hay tối thiểu hóa chi phí.
**Đạo hàm của một hàm hợp là gì?**
- **Trả lời:** Đạo hàm của hàm hợp được tính theo **định lý chuỗi**:
\[
\frac{d}{dx}(f(g(x))) = f'(g(x)) \cdot g'(x)
\]
Tức là, để đạo hàm một hàm hợp, ta lấy đạo hàm của hàm ngoài rồi nhân với đạo hàm của hàm trong.
**Cách tính đạo hàm của một hàm số phân thức là gì?**
- **Trả lời:** Để tính đạo hàm của một hàm phân thức, ta sử dụng **quy tắc đạo hàm của thương**:
\[
\frac{d}{dx} \left( \frac{u(x)}{v(x)} \right) = \frac{v(x) \cdot u'(x) - u(x) \cdot v'(x)}{(v(x))^2}
\]
Trong đó \( u(x) \) và \( v(x) \) là các hàm số, và \( u'(x) \) và \( v'(x) \) là đạo hàm của chúng.
**Đạo hàm của hàm lượng giác như thế nào?**
- **Trả lời:** Các đạo hàm cơ bản của hàm lượng giác bao gồm:
- \( \frac{d}{dx} (\sin x) = \cos x \)
- \( \frac{d}{dx} (\cos x) = -\sin x \)
- \( \frac{d}{dx} (\tan x) = \sec^2 x \)
- \( \frac{d}{dx} (\cot x) = -\csc^2 x \)
- \( \frac{d}{dx} (\sec x) = \sec x \tan x \)
- \( \frac{d}{dx} (\csc x) = -\csc x \cot x \)
**Đạo hàm của hàm số mũ có gì đặc biệt?**
- **Trả lời:** Đạo hàm của một hàm số mũ với cơ số \( e \) (hằng số Euler) là chính nó:
- \( \frac{d}{dx}(e^x) = e^x \)
- Nếu cơ số là một hằng số khác, ta có thể sử dụng công thức:
\[
\frac{d}{dx}(a^x) = a^x \ln a
\]
Trong đó \( a \) là hằng số.
**Công thức đạo hàm của hàm logarit là gì?**
- **Trả lời:** Đạo hàm của hàm logarit tự nhiên (logarit cơ số \( e \)) là:
\[
\frac{d}{dx}(\ln x) = \frac{1}{x}
\]
Đối với logarit có cơ số khác, ta có công thức:
\[
\frac{d}{dx}(\log_a x) = \frac{1}{x \ln a}
\]
Trong đó \( a \) là cơ số của logarit.
**Khi nào một hàm không có đạo hàm?**
- **Trả lời:** Một hàm không có đạo hàm tại một điểm khi:
- Hàm không liên tục tại điểm đó (có gián đoạn).
- Hàm có điểm nhọn (ví dụ: hàm giá trị tuyệt đối tại \( x = 0 \)).
- Đồ thị của hàm có một điểm gãy, tức là không thể vẽ một đường tiếp tuyến duy nhất tại điểm đó.
**Đạo hàm bậc cao là gì?**
- **Trả lời:** Đạo hàm bậc cao là đạo hàm của đạo hàm. Ví dụ, đạo hàm bậc hai của một hàm là đạo hàm của đạo hàm bậc nhất, và nó có thể cung cấp thông tin về độ cong của đồ thị hàm số. Công thức tính đạo hàm bậc hai như sau:
\[
f''(x) = \frac{d}{dx} \left( f'(x) \right)
\]
Đạo hàm bậc cao giúp phân tích tính chất của hàm số, như xác định điểm cực trị hoặc sự thay đổi tốc độ của sự thay đổi.
Bài viết tương tự

27
Tháng 03
Cách chọn size quần áo theo cân nặng sao cho phù hợp
[MỤC LỤC] 1.Cách chọn size quần áo theo cân nặng – cơ bản nhất 2.Các yếu tố cần kết hợp khi chọn size 3.Cách chọn size quần áo khi mua online 4.Mua quần áo ở đâu được ...
Đọc thêm
27
Tháng 03
Hướng dẫn cách chọn size thắt lưng nam phù hợp
[MỤC LỤC] 1.Những size thắt lưng nam cơ bản hiện nay 2.Hướng dẫn Cách chọn size thắt lưng nam phù hợp 3.Mẹo nhỏ khi chọn mua thắt lưng 4.Địa chỉ mua thắt lưng da thậ...
Đọc thêm
27
Tháng 03
Cách phân biệt giày da thật và giả đơn giản, nhanh chóng
[MỤC LỤC] 1.Đặc điểm của da thật và da giả 2.Cách phân biệt giày da thật và giả đơn giản, nhanh chóng 3.Địa chỉ mua giày da thật uy tín, chất lượng 4.Kết luận Cách ...
Đọc thêm



