-
-
-
Tổng tiền thanh toán:
-
Công Thức Hạ Bậc Và Cách Ghi Nhớ Công Thức Lượng Giác
Ngày đăng:
13/12/2024
Bởi: CÔNG TY CỔ PHẦN THƯƠNG MẠI VÀ ĐÀU TƯ -HELIOS
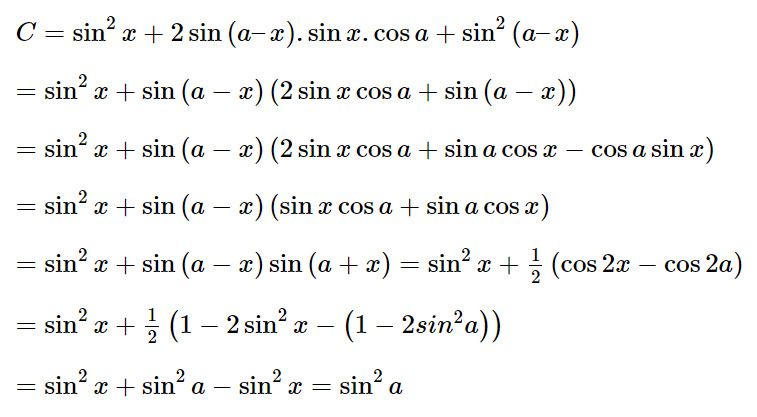
|
[MỤC LỤC]
1. Công thức để hạ bậc trong lượng giác
2. Cách ghi nhớ các công thức trong lượng giác lâu nhất
3. Áp dụng công thức để hạ bậc vào trong cuộc sống
4. Phần mềm và công cụ giúp hỗ trợ học công thức để hạ bậc |
Công thức hạ bậc
1. Công thức để hạ bậc trong lượng giác:

Công thức
2. Cách ghi nhớ các công thức trong lượng giác lâu nhất:
Để ghi nhớ các công thức trong lượng giác lâu dài, bạn có thể áp dụng một số phương pháp học tập hiệu quả sau:
1. Hiểu bản chất công thức
Không chỉ học thuộc lòng: Thay vì chỉ học thuộc lòng công thức, hãy cố gắng hiểu nguồn gốc và cách áp dụng nó. Ví dụ, công thức sin²x + cos²x = 1 là một hệ quả từ định lý Pythagore trong tam giác vuông. Khi bạn hiểu được sự liên kết này, việc ghi nhớ sẽ dễ dàng hơn.
Áp dụng vào thực tế: Hãy tìm cách ứng dụng các công thức trong các bài toán thực tế hoặc trong các ví dụ để thấy rõ sự hữu ích của chúng.
2. Sử dụng phương pháp liên kết
Tạo mối liên kết giữa các công thức: Các công thức trong lượng giác thường có sự liên kết chặt chẽ với nhau. Ví dụ, công thức chuyển đổi giữa sin và cos có thể giúp bạn nhớ các công thức khác. Khi bạn hiểu được một công thức, các công thức liên quan sẽ dễ dàng ghi nhớ hơn.
Hình ảnh hóa: Bạn có thể sử dụng các hình vẽ như tam giác vuông hoặc hình tròn lượng giác để hình dung các công thức. Khi có hình ảnh minh họa, việc nhớ công thức trở nên dễ dàng hơn.
3. Luyện tập thường xuyên
Làm nhiều bài tập: Việc luyện tập đều đặn sẽ giúp bạn nhớ các công thức lâu dài. Khi giải quyết nhiều bài toán, bạn sẽ dần dần nắm vững các công thức và cách áp dụng chúng.
Giải lại bài cũ: Để nhớ lâu, bạn cần thường xuyên ôn lại kiến thức cũ. Hãy giải lại các bài toán từ các bài học trước để củng cố trí nhớ.
4. Chia nhỏ công thức
Phân chia công thức thành phần nhỏ: Chia công thức thành các phần dễ nhớ. Ví dụ, công thức sin(a ± b) = sin(a)cos(b) ± cos(a)sin(b) có thể được nhớ theo từng phần riêng biệt như "sin nhân cos" và "cos nhân sin".
Ghi chú tóm tắt: Tạo một bảng công thức ngắn gọn với các công thức quan trọng. Đặt bảng này ở nơi bạn có thể xem thường xuyên, giúp ôn lại các công thức nhanh chóng.
5. Ứng dụng kỹ thuật mnemotechnics (kỹ thuật ghi nhớ)
Dùng từ viết tắt hoặc hình ảnh: Bạn có thể tạo ra những từ viết tắt hoặc hình ảnh giúp ghi nhớ các công thức. Ví dụ, "SOH CAH TOA" là một cách nhớ các công thức lượng giác cơ bản liên quan đến sin, cos, và tan trong tam giác vuông.
Thực hiện ôn tập theo chu kỳ: Ôn lại các công thức theo lịch trình ôn tập để tăng cường trí nhớ dài hạn. Ví dụ, ôn lại mỗi tuần hoặc mỗi tháng.
6. Học theo nhóm
Học nhóm và thảo luận: Thảo luận về các công thức và cách áp dụng chúng với bạn bè hoặc trong nhóm học tập giúp bạn củng cố và nhớ lâu hơn. Khi giải thích cho người khác, bạn cũng sẽ hiểu rõ hơn và ghi nhớ lâu hơn.
7. Sử dụng ứng dụng học tập
Sử dụng phần mềm hoặc ứng dụng ghi nhớ: Các ứng dụng học tập như Quizlet hoặc Anki giúp bạn ôn tập các công thức theo phương pháp flashcard, tăng cường ghi nhớ và khả năng áp dụng.
8. Lặp lại và ôn tập thường xuyên
Ôn tập liên tục: Khi bạn làm bài tập, cố gắng áp dụng lại các công thức mà bạn đã học, không để chúng phai nhạt theo thời gian. Lặp lại và làm lại bài tập là cách tốt nhất để nhớ lâu.
Chìa khóa để nhớ lâu các công thức trong lượng giác là sự kiên nhẫn, luyện tập đều đặn, và tìm ra phương pháp học phù hợp với bạn.
Tham khảo: ống hdpe tiền phong
3. Áp dụng công thức để hạ bậc vào trong cuộc sống:
Công thức để hạ bậc là một công cụ quan trọng trong lượng giác giúp đơn giản hóa các biểu thức lượng giác có chứa các hàm số bậc cao (như sin²x, cos²x, tan²x…). Việc áp dụng công thức để hạ bậc vào trong cuộc sống có thể giúp giải quyết nhiều vấn đề trong các lĩnh vực khác nhau như kỹ thuật, vật lý, âm nhạc, và thậm chí trong cuộc sống hàng ngày. Dưới đây là một số ví dụ cụ thể về cách áp dụng công thức hạ bậc trong thực tế:

Bài tập ví dụ
1. Ứng dụng trong Kỹ thuật và Vật lý
Dự đoán dao động và sóng: Trong cơ học, sóng và dao động có thể được mô tả bằng các hàm lượng giác, đặc biệt là khi làm việc với dao động điều hòa. Công thức để hạ bậc giúp đơn giản hóa các phương trình này, từ đó làm việc với các dao động dễ dàng hơn. Ví dụ, khi mô tả một sóng có biên độ thay đổi theo thời gian, công thức để hạ bậc có thể giúp rút gọn các phương trình có chứa sin²x, cos²x thành các biểu thức bậc thấp, dễ giải quyết hơn.
Xử lý tín hiệu: Trong lý thuyết tín hiệu, các tín hiệu có thể được mô tả dưới dạng hàm lượng giác. Khi tín hiệu có dạng bậc cao, việc áp dụng công thức để hạ bậc giúp giảm độ phức tạp và dễ dàng phân tích tín hiệu hơn.
>> Tham khảo: Diện tích toàn phần hình trụ
2. Ứng dụng trong Âm nhạc
Xử lý sóng âm: Sóng âm trong âm nhạc có thể được mô tả bởi các hàm lượng giác. Các công thức để hạ bậc có thể giúp giảm độ phức tạp của các tín hiệu âm thanh để dễ dàng phân tích và biến đổi, đặc biệt trong việc tạo ra các hiệu ứng âm thanh trong công nghệ âm nhạc số. Chẳng hạn, khi phân tích các tần số sóng âm hoặc sự thay đổi trong âm thanh, công thức để hạ bậc giúp đơn giản hóa và phân tích dễ dàng hơn.
Hài hòa âm thanh: Khi tạo ra các hợp âm hoặc tạo hiệu ứng âm thanh từ các sóng cơ bản, công thức để hạ bậc giúp điều chỉnh các thành phần sóng, từ đó tạo ra các âm thanh có sự kết hợp hài hòa.
3. Ứng dụng trong Công nghệ và Máy tính
Xử lý ảnh: Trong xử lý ảnh, việc áp dụng công thức để hạ bậc giúp đơn giản hóa các hàm lượng giác sử dụng trong các bộ lọc, giúp xử lý và phân tích hình ảnh dễ dàng hơn, đặc biệt khi làm việc với các hình ảnh sóng hoặc các sóng ngắn trong kỹ thuật đồ họa.
Mô phỏng và mô hình hóa: Khi mô phỏng các hiện tượng vật lý trong máy tính (như sóng, dao động), công thức để hạ bậc giúp đơn giản hóa các phương trình và cải thiện tốc độ tính toán.
4. Ứng dụng trong Điều khiển và Cảm biến
Điều khiển tự động: Trong các hệ thống điều khiển tự động (như robot, máy bay không người lái), công thức để hạ bậc có thể được áp dụng để giảm độ phức tạp của các tín hiệu đầu vào, giúp cải thiện quá trình điều khiển và tối ưu hóa phản ứng của hệ thống đối với các tín hiệu và dao động.
Cảm biến sóng: Trong các cảm biến sử dụng sóng điện từ hoặc sóng siêu âm để đo đạc, công thức để hạ bậc có thể giúp đơn giản hóa các phép tính khi phân tích dữ liệu thu thập từ các cảm biến này.
5. Ứng dụng trong Vật lý thực tế
Quá trình tán xạ sóng: Khi nghiên cứu sự tán xạ của sóng (chẳng hạn như sóng âm, sóng ánh sáng), các công thức để hạ bậc có thể giúp đơn giản hóa các phương trình mô tả quá trình này. Ví dụ, khi tính toán sóng phản xạ và khúc xạ trong vật lý, công thức để hạ bậc giúp giảm độ phức tạp của các hàm sin và cos bậc cao.
Tính toán lực trong cơ học: Trong một số bài toán về lực trong cơ học, việc áp dụng công thức để hạ bậc có thể giúp giảm bớt các biểu thức phức tạp và dễ dàng tính toán lực và chuyển động trong các hệ thống cơ học.
6. Ứng dụng trong Kỹ thuật Cơ khí và Điện
Phân tích dao động cơ học: Trong kỹ thuật cơ khí, các hệ thống dao động có thể được mô phỏng bằng các phương trình lượng giác phức tạp. Công thức để hạ bậc giúp đơn giản hóa các phương trình này, giúp các kỹ sư dễ dàng phân tích và thiết kế hệ thống.
Điện tử và mạch điện: Trong các mạch điện có chứa các thành phần như tụ điện và cuộn cảm, các công thức lượng giác có thể được sử dụng để mô tả các sóng điện từ. Việc áp dụng công thức hạ bậc giúp giảm độ phức tạp của các phương trình và dễ dàng tính toán các đặc tính của mạch.
7. Ứng dụng trong Toán học và Giải trí
Giải quyết các bài toán trắc nghiệm: Các công thức để hạ bậc có thể giúp giải nhanh các bài toán trắc nghiệm trong các kỳ thi hoặc trong việc giải quyết các bài toán toán học. Việc sử dụng công thức để hạ bậc giúp rút gọn các biểu thức và làm bài toán trở nên dễ dàng hơn.
Giải trí: Trong các trò chơi hoặc ứng dụng giải trí có liên quan đến mô phỏng vật lý, như các trò chơi mô phỏng sóng hoặc chuyển động, công thức để hạ bậc giúp đơn giản hóa các mô hình toán học phức tạp, làm cho quá trình tính toán nhanh hơn và trò chơi mượt mà hơn.
Tóm lại, công thức hạ bậc không chỉ có giá trị lý thuyết mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, đặc biệt là trong khoa học, kỹ thuật và công nghệ. Việc sử dụng công thức này giúp đơn giản hóa các tính toán, làm tăng hiệu quả và tính chính xác trong các ứng dụng thực tế.
Tham khảo: báo giá ống nhựa hdpe
4. Phần mềm và công cụ giúp hỗ trợ học công thức để hạ bậc:
Để hỗ trợ việc học và áp dụng các công thức để hạ bậc, có nhiều phần mềm và công cụ có thể giúp bạn làm việc hiệu quả hơn. Dưới đây là một số phần mềm và công cụ học tập hữu ích trong việc giải quyết các bài toán lượng giác, đặc biệt là công thức để hạ bậc
1. Wolfram Alpha
Mô tả: Là một công cụ tìm kiếm tính toán mạnh mẽ, Wolfram Alpha có thể giải quyết hầu hết các bài toán lượng giác, bao gồm các phép tính với công thức hạ bậc. Bạn chỉ cần nhập một biểu thức lượng giác, và công cụ này sẽ giúp bạn tính toán, rút gọn hoặc chuyển đổi các công thức.
Chức năng: Tính toán, giải phương trình, rút gọn biểu thức lượng giác, chuyển đổi giữa các dạng công thức.
2. GeoGebra
Mô tả: GeoGebra là một phần mềm toán học mạnh mẽ giúp bạn trực quan hóa các hàm số lượng giác, vẽ đồ thị và thực hiện các phép tính lượng giác. Với GeoGebra, bạn có thể vẽ các đồ thị của các hàm sin, cos, tan và thấy cách các công thức để hạ bậc hoạt động trực quan.
Chức năng: Vẽ đồ thị, tính toán lượng giác, hỗ trợ học tập và nghiên cứu toán học với các công thức để hạ bậc.
3. Desmos
Mô tả: Desmos là một công cụ vẽ đồ thị online nổi tiếng, hỗ trợ vẽ các đồ thị hàm lượng giác và thực hiện các phép tính liên quan đến lượng giác. Desmos giúp bạn nhìn thấy mối quan hệ giữa các hàm số, và bạn có thể dễ dàng thấy được sự thay đổi khi áp dụng công thức để hạ bậc.
Chức năng: Vẽ đồ thị, giải bài toán lượng giác, hỗ trợ phân tích các hàm lượng giác.

Cách giải
4. Microsoft Math Solver
Mô tả: Đây là một công cụ miễn phí của Microsoft giúp giải các bài toán toán học, trong đó có các bài toán lượng giác. Bạn có thể quét hình ảnh bài toán hoặc nhập trực tiếp các biểu thức, và phần mềm sẽ giúp bạn giải các phương trình lượng giác, bao gồm việc áp dụng công thức để hạ bậc.
Chức năng: Giải phương trình toán học, rút gọn biểu thức, hỗ trợ học toán và lượng giác.
5. SymPy (Python Library)
Mô tả: SymPy là một thư viện Python mạnh mẽ cho tính toán biểu thức đại số, bao gồm cả lượng giác. Bạn có thể sử dụng SymPy để giải các bài toán lượng giác và áp dụng công thức để hạ bậc trong Python.
Chức năng: Tính toán, giải phương trình, áp dụng công thức lượng giác, làm việc với biểu thức lượng giác.
6. Cymath
Mô tả: Cymath là một ứng dụng di động và web giúp giải quyết các bài toán toán học, bao gồm cả lượng giác. Bạn chỉ cần nhập biểu thức lượng giác, và Cymath sẽ giúp bạn giải quyết và rút gọn biểu thức, bao gồm việc áp dụng công thức để hạ bậc.
Chức năng: Giải phương trình, rút gọn biểu thức, học toán và lượng giác.
7. Anki (Flashcard)
Mô tả: Anki là phần mềm học qua flashcard, giúp bạn ghi nhớ các công thức, trong đó có công thức để hạ bậc, qua việc ôn tập lặp lại. Bạn có thể tạo bộ thẻ flashcard riêng với các công thức để hạ bậc và ôn tập thường xuyên để ghi nhớ lâu dài.
Chức năng: Học thông qua flashcard, ôn tập các công thức toán học.
8. Matlab
Mô tả: Matlab là một phần mềm tính toán kỹ thuật mạnh mẽ, thường được sử dụng trong nghiên cứu khoa học và kỹ thuật. Matlab có thể giúp bạn giải quyết các bài toán liên quan đến lượng giác, đặc biệt là khi làm việc với các biểu thức bậc cao cần phải áp dụng công thức để hạ bậc.
Chức năng: Tính toán, giải phương trình, xử lý tín hiệu và dữ liệu, mô phỏng các hiện tượng vật lý.
9. Sine, Cosine, Tangent - Trắc nghiệm trực tuyến
Mô tả: Các công cụ trắc nghiệm trực tuyến như Khan Academy hoặc Brilliant.org giúp bạn luyện tập và áp dụng các công thức để hạ bậc trong lượng giác qua các bài tập và câu hỏi tương tác. Các bài tập này giúp bạn hiểu rõ hơn về cách thức hoạt động của công thức và ứng dụng chúng trong các bài toán thực tế.
10. LaTeX (Soạn thảo công thức)
Mô tả: LaTeX là phần mềm soạn thảo văn bản và công thức toán học, cho phép bạn tạo ra các công thức lượng giác chuyên nghiệp. Bạn có thể soạn thảo các công thức hạ bậc một cách chính xác và rõ ràng để học và tham khảo.
Chức năng: Soạn thảo công thức toán học, viết các biểu thức lượng giác.
Lời khuyên khi sử dụng các công cụ học tập:
Kết hợp giữa lý thuyết và thực hành: Chỉ sử dụng phần mềm khi bạn đã hiểu rõ lý thuyết, để từ đó sử dụng công cụ một cách hiệu quả.
Thực hành thường xuyên: Các công cụ chỉ hỗ trợ bạn trong việc thực hiện phép tính, nhưng chính việc luyện tập nhiều sẽ giúp bạn ghi nhớ các công thức để hạ bậc lâu dài.
Hy vọng rằng những phần mềm và công cụ này sẽ giúp bạn học tập và áp dụng công thức hạ bậc một cách hiệu quả!
Bài viết tương tự
13
Tháng 12
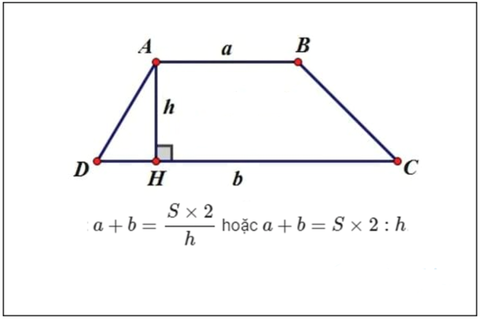
Cách Tính Và Công Thức Tính Diện Tích Hình Thang
[MỤC LỤC] 1. Công thức tính diện tích hình thang 2. 10 đề bài thường gặp sử dụng công thức tính diện tích hình thang 3. Các ví dụ về đồ vật có hi...
Đọc thêm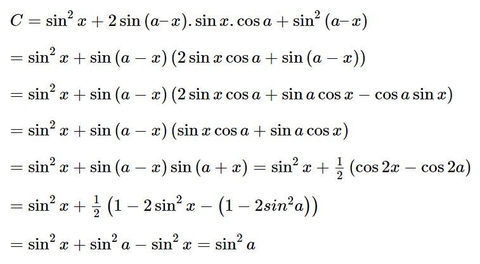
13
Tháng 12
Công Thức Hạ Bậc Và Cách Ghi Nhớ Công Thức Lượng Giác
[MỤC LỤC] 1. Công thức để hạ bậc trong lượng giác 2. Cách ghi nhớ các công thức trong lượng giác lâu nhất 3. Áp dụng công thức để hạ bậc va...
Đọc thêm
13
Tháng 12
Phân Tích Vị Trí Nốt Ruồi Trên Mặt Nữ Về Nhân Tướng Học
[MỤC LỤC] 1. Vì sao phải phân tích các vị trí nốt ruồi trên mặt phụ nữ? 2. Ý nghĩa của một số vị trí nốt ruồi trên mặt nữ thường gặp 3. Như...
Đọc thêm



