-
-
-
Tổng tiền thanh toán:
-
Dấu hiệu nhận biết và công thức tính diện tích hình thang là gì?
Ngày đăng:
29/10/2024
Bởi: CÔNG TY CỔ PHẦN THƯƠNG MẠI VÀ ĐÀU TƯ -HELIOS
|
[MỤC LỤC]
|
Công thức tính diện tích hình thang
1. Hình thang là gì
Hình thang là gì?
Một tứ giác chỉ cần có 2 cạnh đối diện song song với nhau thì đó là hình thang. Hai cạnh song song đó người ta gọi là đáy hình thang, còn 2 cạnh còn lại được gọi là cạnh bên.
Các yếu tố của hình thang
Đáy lớn: Cạnh đáy có độ dài lớn hơn.
Đáy nhỏ: Cạnh đáy có độ dài nhỏ hơn.
Cạnh bên: Hai cạnh không song song với nhau.
Chiều cao: Đoạn thẳng vuông góc kẻ từ một điểm trên đáy lớn đến đáy nhỏ.
Ứng dụng của hình thang
Hình thang xuất hiện rất nhiều trong cuộc sống hàng ngày và các lĩnh vực khác nhau như:
Kiến trúc: Các mái nhà, cửa sổ, cầu thang... thường có dạng hình thang.
Xây dựng: Các khung cửa, cột nhà...
Đường xá: Các đoạn đường đèo, cầu...
Và nhiều lĩnh vực khác…
Hình thang có 2 cạnh đối diện song song
2. Tính chất của hình thang
Tính chất về cạnh
Nếu một hình thang có hai đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
Ngược lại, nếu một hình thang có hai cạnh bên song song thì chúng bằng nhau và hai đáy cũng bằng nhau.
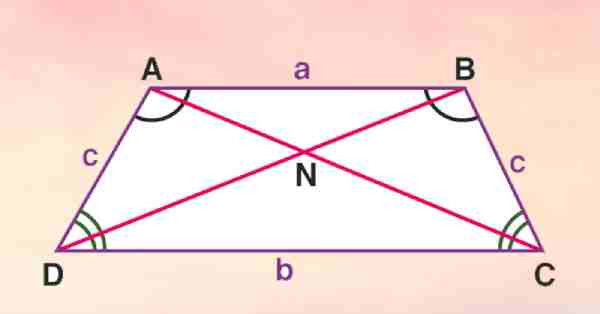
Đặc biệt, hình thang có 2 đường chéo bằng nhau được gọi là hình thang cân.
Tính chất về góc
Hai góc kề một cạnh bên của hình thang có tổng 2 góc bằng 180 độ.
Đặc biệt, trong hình thang cân, 2 góc kề cạnh đáy sẽ bằng nhau.
Đường trung bình của hình thang
Đường trung bình của hình thang là đoạn thẳng nối từ trung điểm hai cạnh bên. Đường trung bình của hình thang có các tính chất sau:
Song song với hai đáy.
Bằng nửa tổng hai đáy.
3. Hình thang đặc biệt
Hình thang cân
Định nghĩa: Hình thang cân trước tiên là hình thang, và có hai cạnh bên bằng nhau.
Tính chất:
Hai góc kề một đáy bằng nhau.
Hai đường chéo bằng nhau.
Đường trung bình song song với hai đáy và bằng nửa tổng hai đáy (tính chất này chung cho mọi hình thang).
Ví dụ: Mái nhà, cầu thang,... thường có hình dáng của một hình thang cân.
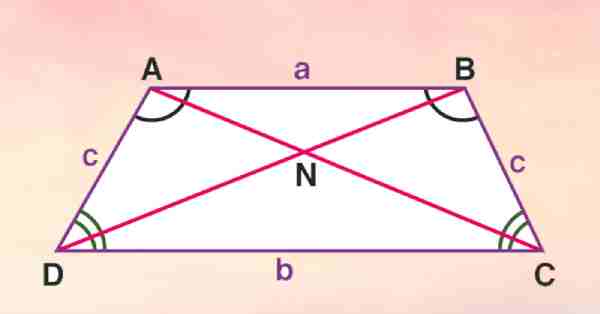
Hình thang cân
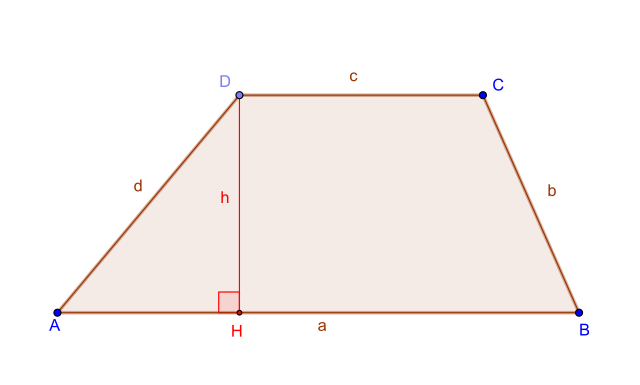
Hình thang vuông
Định nghĩa: Hình thang vuông là hình thang, có một góc vuông nằm ở góc bất kỳ.
Tính chất:
Cạnh bên vuông góc với một trong hai đáy.
Các góc còn lại của hình thang vuông có thể tính được dựa vào tính chất tổng các góc trong một tứ giác.
Ví dụ: Một phần của khung cửa sổ, một số loại hộp,... có thể có dạng hình thang vuông.
Tham khảo: Bảng chữ cái tiếng Việt
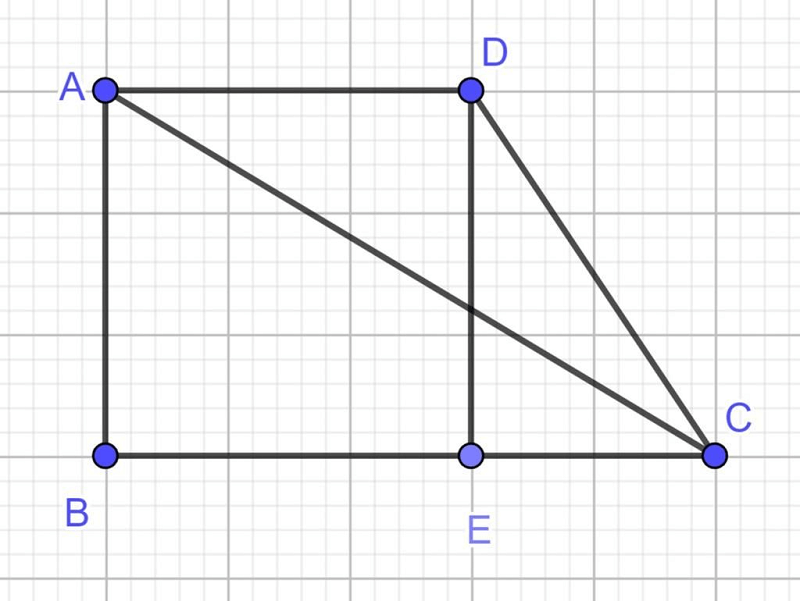
Hình thang vuông
Hình thang đều
Định nghĩa: Hình thang đều là hình thang vừa là hình thang cân vừa là hình thang vuông.
Tính chất:
Cả hai góc kề một đáy đều bằng 90 độ.
Hai cạnh bên bằng nhau và vuông góc với hai đáy.
Hai đường chéo bằng nhau và vuông góc với nhau.
Ví dụ: Ít gặp trong thực tế, nhưng hình thang đều thường được sử dụng trong các bài toán hình học để minh họa các tính chất.
Những điều thú vị khác về hình thang
Hình thang có đường trung bình: Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên. Đường trung bình song song với hai đáy và bằng nửa tổng hai đáy.
Diện tích hình thang: Diện tích hình thang bằng tích của đường cao và trung bình cộng của hai đáy.
Bạn có muốn tìm hiểu thêm về các bài toán liên quan đến hình thang đặc biệt không? Hoặc bạn có câu hỏi nào về chủ đề này, đừng ngần ngại đặt ra nhé!
Từ khóa: hình thang, hình thang cân, hình thang vuông, hình thang đều, tính chất hình thang, toán học
Lưu ý: Để hiểu rõ hơn về các khái niệm và tính chất, bạn nên kết hợp việc đọc lý thuyết với việc vẽ hình và làm bài tập.
4. Tìm hiểu về công thức tính diện tích hình thang
Hình thang là gì?
Trước khi đi sâu vào công thức, chúng ta cùng ôn lại khái niệm về hình thang. Hình thang là một tứ giác lồi, có 2 cạnh đối diện song song với nhau. Hai cạnh song song này gọi là hai đáy của hình thang, còn hai cạnh còn lại gọi là hai cạnh bên.
Công thức diện tích hình thang
Diện tích của một hình thang được tính bằng công thức sau:
S = (a + b) x h / 2
Trong đó:
S: Diện tích hình thang
a: Độ dài đáy lớn
b: Độ dài đáy bé
h: Chiều cao của hình thang (đoạn thẳng vuông góc với hai đáy)
Giải thích công thức:
(a + b): Ta tính tổng độ dài hai đáy.
(a + b) x h: Tích của tổng độ dài hai đáy và chiều cao sẽ cho ta diện tích của một hình chữ nhật có chiều dài bằng tổng hai đáy và chiều rộng bằng chiều cao của hình thang.
(a + b) x h / 2: Vì hình thang chỉ là một nửa của hình chữ nhật vừa tạo thành, nên ta chia kết quả cho 2 để được diện tích hình thang.
Ví dụ minh họa
Giả sử chúng ta có một hình thang với:
Đáy lớn (a) = 10cm
Đáy bé (b) = 6cm
Chiều cao (h) = 8cm
Diện tích hình thang sẽ là: S = (10 + 6) x 8 / 2 = 64 cm²
Tại sao công thức này lại đúng?
Để hiểu rõ hơn về công thức, bạn có thể chia hình thang thành các hình tam giác và hình chữ nhật đơn giản hơn, sau đó tính tổng diện tích các hình đó. Bạn sẽ thấy rằng kết quả thu được vẫn giống với công thức trên.
Ứng dụng của công thức diện tích hình thang
Công thức diện tích hình thang có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Xây dựng: Tính diện tích các bức tường, mái nhà có hình thang.
Thiết kế: Tính diện tích các hình dạng phức tạp được tạo thành từ nhiều hình thang nhỏ.
Địa lý: Tính diện tích các khu đất có hình dạng bất thường.
Công thức diện tích hình thang là một công cụ hữu ích giúp chúng ta giải quyết nhiều bài toán thực tế. Bằng cách hiểu rõ công thức và cách áp dụng, bạn sẽ tự tin hơn trong việc giải quyết các bài toán liên quan đến hình thang.
Trên đây là một số thông tin về chủ đề hình thang và công thức tính diện tích hình thang. Hi vọng các bạn đã có cho mình thông tin hữu ích.
Bài viết tương tự
13
Tháng 12
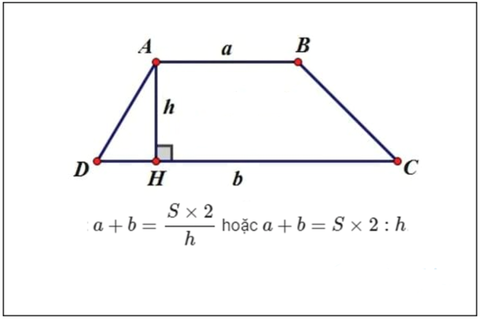
Cách Tính Và Công Thức Tính Diện Tích Hình Thang
[MỤC LỤC] 1. Công thức tính diện tích hình thang 2. 10 đề bài thường gặp sử dụng công thức tính diện tích hình thang 3. Các ví dụ về đồ vật có hi...
Đọc thêm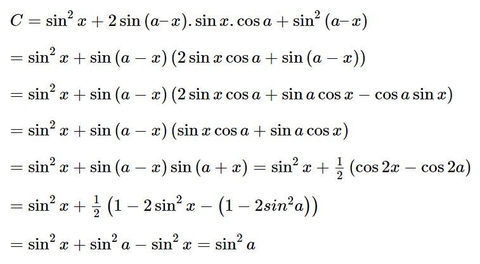
13
Tháng 12
Công Thức Hạ Bậc Và Cách Ghi Nhớ Công Thức Lượng Giác
[MỤC LỤC] 1. Công thức để hạ bậc trong lượng giác 2. Cách ghi nhớ các công thức trong lượng giác lâu nhất 3. Áp dụng công thức để hạ bậc va...
Đọc thêm
13
Tháng 12
Phân Tích Vị Trí Nốt Ruồi Trên Mặt Nữ Về Nhân Tướng Học
[MỤC LỤC] 1. Vì sao phải phân tích các vị trí nốt ruồi trên mặt phụ nữ? 2. Ý nghĩa của một số vị trí nốt ruồi trên mặt nữ thường gặp 3. Như...
Đọc thêm



