-
-
-
Tổng tiền thanh toán:
-
Tổng hợp các công thức hạ bậc lượng giác đầy đủ, chi tiết
Ngày đăng:
28/10/2024
Bởi: CÔNG TY CỔ PHẦN THƯƠNG MẠI VÀ ĐÀU TƯ -HELIOS

|
[MỤC LỤC]
|
Công thức hạ bậc
1. Công thức hạ bậc là gì
Công thức lượng giác hạ bậc là gì?
Công thức lượng giác hạ bậc là một tập hợp các công thức toán học giúp chúng ta chuyển đổi các biểu thức lượng giác có bậc cao (như sin²x, cos²x, ...) về dạng các biểu thức đơn giản hơn, thường là các biểu thức bậc nhất đối với cos hoặc sin. Nói một cách dễ hiểu, công thức lượng giác hạ bậc giúp chúng ta "hạ" bậc của các biểu thức lượng giác phức tạp, giúp việc tính toán trở nên đơn giản hơn.

Công thức lượng giác hạ bậc
2. 7 công thức hạ bậc lượng giác cơ bản
Công thức bình phương sin
sin²x = (1 - cos2x) / 2
Công thức bình phương cos
cos²x = (1 + cos2x) / 2
Công thức bình phương tan
tan²x = (1 - cos2x) / (1 + cos2x)
Công thức sin2x
sin2x = 2sinxcosx
Công thức cos2x
cos2x = cos²x - sin²x = 2cos²x - 1 = 1 - 2sin²x
Công thức tan2x
tan2x = (2tanx) / (1 - tan²x)
Công thức cot2x
cot2x = (cot²x - 1) / (2cotx)
Lưu ý
Các công thức trên giúp ta chuyển các biểu thức lượng giác có bậc cao về bậc thấp hơn, thường là bậc một.
Việc sử dụng thành thạo các công thức này sẽ giúp bạn giải quyết nhanh chóng và chính xác các bài toán lượng giác.
Ngoài ra, còn có nhiều công thức khác phức tạp hơn, nhưng thường được suy ra từ 7 công thức cơ bản trên.
Tham khảo:
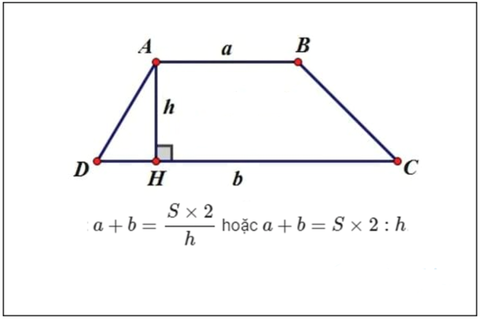
Công thức tính diện tích hình thang
Một số ví dụ về việc áp dụng công thức
Đơn giản hóa biểu thức:
Ví dụ: Biểu thức sin⁴x + cos⁴x có thể đơn giản hóa bằng cách sử dụng công thức bình phương sin và cos.
Giải phương trình lượng giác:
Ví dụ: Phương trình 2cos²x - 3sinx + 1 = 0 có thể giải bằng cách sử dụng công thức cos²x.
Tính tích phân:
Ví dụ: Tích phân ∫sin²xdx có thể tính bằng cách sử dụng công thức sin²x.
Tham khảo: Bảng chữ cái tiếng nhật

Công thức lượng giác hạ bậc
3. Bài tập cơ bản về công thức lượng giác hạ bậc cơ bản
Công thức lượng giác hạ bậc cơ bản
sin²α = (1 - cos2α)/2
cos²α = (1 + cos2α)/2
tan²α = (1 - cos2α)/(1 + cos2α)
Ví dụ 1: Rút gọn biểu thức
A = sin²x + cos²x
Giải: Áp dụng công thức lượng giác hạ bậc, ta có: A = (1 - cos2x)/2 + (1 + cos2x)/2 = (1 + 1)/2 = 1 Vậy A = 1
Ví dụ 2: Tính giá trị biểu thức
B = 3sin²45° - 2cos²60°
Giải: Áp dụng công thức lượng giác hạ bậc, ta có: B = 3*(1 - cos90°)/2 - 2*(1 + cos120°)/2 Vì cos90° = 0 và cos120° = -1/2, nên: B = 3*(1 - 0)/2 - 2*(1 - 1/2)/2 = 3/2 - 1/2 = 1 Vậy B = 1
Ví dụ 3: Chứng minh đẳng thức
sin⁴x - cos⁴x = 2sin²x - 1
Giải: Biến đổi vế trái: sin⁴x - cos⁴x = (sin²x)² - (cos²x)² Áp dụng hằng đẳng thức a² - b² = (a + b)(a - b), ta có: = (sin²x + cos²x)(sin²x - cos²x) Vì sin²x + cos²x = 1, nên: = sin²x - cos²x Áp dụng công thức, ta có: = (1 - cos2x)/2 - (1 + cos2x)/2 = -cos2x Biến đổi vế phải: 2sin²x - 1 = 2*(1 - cos2x)/2 - 1 = -cos2x Vậy vế trái bằng vế phải, đẳng thức được chứng minh.
Các bài tập nâng cao:
Bài toán liên quan đến góc nhân đôi: Sử dụng công thức để giải các phương trình lượng giác, bất phương trình lượng giác có chứa góc nhân đôi.
Bài toán liên quan đến góc chia đôi: Áp dụng công thức để rút gọn biểu thức chứa căn thức của hàm lượng giác.
Bài toán tổng hợp: Kết hợp công thức với các công thức lượng giác khác để giải các bài toán phức tạp hơn.
Lưu ý:
Ôn lại các công thức lượng giác cơ bản: Để làm tốt các bài tập về công thức, bạn cần nắm vững các công thức lượng giác như sin(a+b), cos(a-b), tan(a+b),...
Rèn luyện kỹ năng biến đổi biểu thức: Việc thành thạo các kỹ năng biến đổi biểu thức sẽ giúp bạn giải quyết nhanh chóng các bài toán.
Làm nhiều bài tập: Càng làm nhiều bài tập, bạn càng quen thuộc với các dạng bài và cách giải.
>> Xem thêm: Diện tích toàn phần hình trụ

Công thức lượng giác hạ bậc
4. Cách ghi nhớ công thức lượng giác hạ bậc
Hiểu rõ bản chất
Hạ bậc là gì: Trước hết, hãy hiểu rõ ý nghĩa của việc hạ bậc. Đó là quá trình biến đổi các biểu thức lượng giác có bậc cao (như sin^2x, cos^2x) về dạng bậc thấp hơn (như 1/2 - 1/2cos2x).
Ứng dụng: Hiểu được ứng dụng của công thức lượng giác hạ bậc trong việc giải các bài toán lượng giác sẽ giúp bạn hứng thú hơn trong việc học thuộc lòng.
Các mẹo ghi nhớ
Tạo câu thần chú: Tự tạo ra những câu thần chú ngắn gọn, dễ nhớ liên kết các công thức với nhau. Ví dụ: "Cos bình nửa trừ nửa cos gấp đôi" để nhớ công thức cos^2x = (1+cos2x)/2.
Liên kết với hình ảnh: Tưởng tượng các hình ảnh liên quan đến công thức. Ví dụ, hình ảnh một cái thang để nhớ công thức tanx = sinx/cosx.
Nhóm công thức: Nhóm các công thức có cấu trúc tương tự nhau để dễ dàng ghi nhớ.
Áp dụng thường xuyên: Thực hành giải bài tập thường xuyên sẽ giúp bạn ghi nhớ công thức một cách tự nhiên.
Sử dụng sơ đồ tư duy: Vẽ sơ đồ tư duy để hệ thống hóa các công thức và mối quan hệ giữa chúng.
Tham khảo: giá ống hdpe d200
Một số mẹo nhỏ khác
Viết lại công thức nhiều lần: Việc viết đi viết lại các công thức sẽ giúp bạn ghi nhớ sâu hơn.
Giải thích cho người khác: Khi giải thích cho người khác, bạn sẽ hiểu rõ hơn về công thức và nhớ lâu hơn.
Tìm kiếm những bài hát, video vui nhộn về công thức lượng giác: Điều này sẽ giúp bạn học tập một cách thú vị hơn.
Công thức lượng giác hạ bậc cơ bản
Để bắt đầu, bạn nên tập trung vào các công thức lượng giác hạ bậc cơ bản sau:
cos^2x = (1+cos2x)/2
sin^2x = (1-cos2x)/2
2sinxcosx = sin2x
Nguồn tài liệu tham khảo
Sách giáo khoa: Tham khảo sách giáo khoa để có những lời giải thích chi tiết và ví dụ minh họa.
Video trên Youtube: Có rất nhiều video hướng dẫn về công thức lượng giác hạ bậc lượng giác trên Youtube.
Các diễn đàn toán học: Tham gia các diễn đàn để hỏi đáp và trao đổi kinh nghiệm với các bạn khác.
Trên đây là một số thông tin về công thức lượng giác hạ bậc. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.
Bài viết tương tự
13
Tháng 12
Cách Tính Và Công Thức Tính Diện Tích Hình Thang
[MỤC LỤC] 1. Công thức tính diện tích hình thang 2. 10 đề bài thường gặp sử dụng công thức tính diện tích hình thang 3. Các ví dụ về đồ vật có hi...
Đọc thêm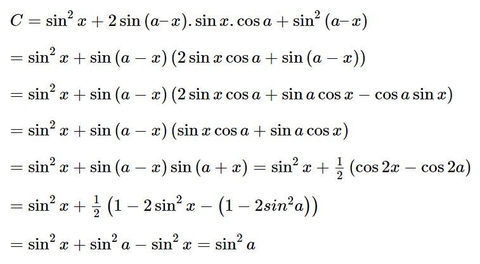
13
Tháng 12
Công Thức Hạ Bậc Và Cách Ghi Nhớ Công Thức Lượng Giác
[MỤC LỤC] 1. Công thức để hạ bậc trong lượng giác 2. Cách ghi nhớ các công thức trong lượng giác lâu nhất 3. Áp dụng công thức để hạ bậc va...
Đọc thêm
13
Tháng 12
Phân Tích Vị Trí Nốt Ruồi Trên Mặt Nữ Về Nhân Tướng Học
[MỤC LỤC] 1. Vì sao phải phân tích các vị trí nốt ruồi trên mặt phụ nữ? 2. Ý nghĩa của một số vị trí nốt ruồi trên mặt nữ thường gặp 3. Như...
Đọc thêm



